Dies ist mein Mathereferat aus dem 12. Jahrgang. Das Inhaltsverzeichnis ist leider nicht mehr aufzufinden
Das sind in der Mathematik Anordnungen von Objekten, die aus einer gegebenen Menge genommen sind. Permutationen spielen in vielen Bereichen der Mathematik eine wichtige Rolle, z. B. bei der Binomialentwicklung sowie in der Wahrscheinlichkeitstheorie und Statistik, wo sie verwendet werden können, um die Anzahl möglicher Anordnungen eines Systems zu berechnen. Die Kombinatorik hat ihre Grundlagen in den Formeln für Permutationen und Kombinationen. Sie hat u. a. wichtige Anwendungen in der Entwicklung und im Betrieb von Computern. Insgesamt ist die Theorie der Permutationen und Kombinationen überall dort von Nutzen, wo die möglichen Anordnungen einer endlichen Anzahl von Elementen eine Rolle spielen.
1. ) Permutationen
Permutationen sind Anordnungen von einer Bestimmten Menge {a1, a2, a3, ... an.}, wobei Reihenfolge berücksichtigt wird. In jeder neue Anordnung darf nur jedes Element nur eine mal vorkommen.
Als Beispiel betrachte man eine Trommel mit 4 Kugeln. Die Anordnung, in der die Kugeln gezogen werden, wäre eine Permutation. Man kann insgesamt 24 solche Anordnungen (Kombinationen) entwickeln:
Augabe 1:
Schreibe die 24 Permutationen der Elemente a1, a2, a3, a4 übersichtlich an.
(...)
-3-
Bei 4 Elementen gibt es 24 Permutationen, man kann hinter das erste Element jeweils die 6 Permutationen hinterschreiben, die die restlichen drei Elemente bilden können.
Die Anzahl der verschiedenen Permutationen kann man herleiten, indem man betrachtet, was beim ziehen der Kugeln geschieht. Die erste gemischte und gezogene Kugel könnte eine von vier möglichen Kugeln sein. Für die zweite Kugel bleiben nur noch drei Möglichkeiten übrig, für die dritte Kugel zwei, und die vierte Kugel wäre dann festgelegt. Also erhält man insgesamt 4 × 3 × 2 × 1 = 24 Anordnungen. Dies kann auch in der Form 4! - lies "vier Fakultät" - geschrieben werden.
Es brachn folglich nur die Elemente miteinander multiplirirt werden,
z.B.![]()
VI ) Die Anzahl der Permutationen von n (unentliche Zahl) verschiedenen Elementen a1, a2, a3, ..., an ist

![]()
![]() (beweiß siehe Aufgabe 2)
(beweiß siehe Aufgabe 2)
Dieses kann man durch n! abkürzen. Pn = n! ( n!: lies: n Fakultät)
Bei Element aus ![]() wird wie in II beschrieben für n die Anzahl der Elememte eingesetzt z.B.
wird wie in II beschrieben für n die Anzahl der Elememte eingesetzt z.B.
1! = 1 bei einem Element gibt es nur eine Möglichkeit der Permutation

Für die 0! ist als 1 Permutation Diffinirt
-4-
Möglich Aufgaben zur Permutationen im Untericht:
2.)Führe den Beweis von VI mit vollständiger Induktion durch.
1. Induktionsanfang:
![]()
für 1! = 1(1-1)!
= 1(0)!
=![]() =1
(w)
=1
(w)
2 Induktionsschritt:

3.) a) Berechne 7! und 10! b) Wieviel Stellen hat die Zahl 20! ?
7! = 5040 2,4...18 =19 Stellen
10! = 3628800
4.) Wieviel Tonfolgen von je 8 Tönen erlauben die 8 Töne der C-Dur-Tonleiter, wenn keiner der Töne mehrfach vorkommt ?
40320Tonfolgen
5.) Wieviel Möglichkeiten bezüglich der Reihenfolge gibt es beim Aufrufen von 16 Schülern, wenn jedern genau einmal drankommen soll ?
1,90207180812 Möglichkeiten
-5-
6.) Rechne a) ![]()
a) = 30 b) = 840 c) = ![]()
d) =
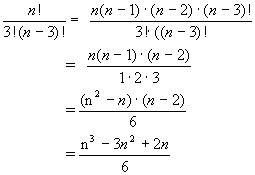
-6-
Kombinationen
Kombinationen sind Anordnungen von Objekten ohne Beachtung der Reihenfolge.
Veranschaulichung:
Aus einer trommel mit 5 Kugeln, will man 3 ziehen und so ein Losverfahren für z.B eine kleine Tombula organisiren. Es ist die reihenfolge, wie bei lotto, der gezogenen kugeln unwichtig.
Bei dem ziehen der 1. Kugel gibt es 5 Möglichkeiten, weil jede kugel gezogen werden kann.
Bei der Ziehung der 2. Kugel gibt es nur noch Möglichkeiten, da nur noch 4 in der Trommel vorhanden sind.
Die 3. hat noch 3 Möglichkeiten.
Daraus folgt in der Veranschaulichten Darstellung: (...)
Die aber reihenfolgenabhängig sind, um die Kombination
abzuziehen, die die gleichen Zahlen haben in unterschidlicher reihenfolge, müß
das ergebnis (60) durch die Anzahl der gezogenen Zahlen (3) dividirt werden
und auch zur fakultät genommen werden (3!) Þ ![]()
Eine nubestimmte Anzahl von Zahlen (k) aus einer ebenfals
unbestimmten Menge (n) ![]() ,
wird als Kombination der n Elemente zu je k bezeichnet. Z.B 2,4,1 ist
eine Kombination der 4 Elemente (1,2,3,4) zu je 3 Elementen
,
wird als Kombination der n Elemente zu je k bezeichnet. Z.B 2,4,1 ist
eine Kombination der 4 Elemente (1,2,3,4) zu je 3 Elementen
Veranschaulichung:
a1, a2, a3,
a4, a5, ..., ak1 ..., an Þ
![]() =
=![]()
n
x (n-1) [n- (k+1) ]
x (n-2)
-7-
Die Anzahl der Kombination von
n verschiedenen Elememten zu je k Elementen ist bei Berücksichtigung der Anordnung:
K Die Anzahl der Kombination
von n verschiedenen Elememten zu je k Elementen ist bei Berücksichtigung der
Anordnung: K Die Anzahl der Kombination
von n verschiedenen Elememten zu je k Elementen ist bei Berücksichtigung der
Anordnung: K Die Anzahl der Kombination
von n verschiedenen Elememten zu je k Elementen ist bei Berücksichtigung der
Anordnung: K Die Anzahl der Kombination
von n verschiedenen Elememten zu je k Elementen ist bei Berücksichtigung der
Anordnung: KI =![]() ( I )
( I )
ohne Berücksichtigung der Anordnung: KII
=![]() ( II )
( II )
Der lerztere Term ( II ) kommt in der Mathematik sehr oft vor man hat daher eine Abkürzung für ihn eingeführt und schreibt:
![]() ,
(lies: n über k), (nÎ N, 0 <
k £ n)
,
(lies: n über k), (nÎ N, 0 <
k £ n)
Es folgt
1.)![]()
2.)![]() weil, 0! = 1 ist
weil, 0! = 1 ist
3.)![]()
Praktische anweisung:
![]()
-8-
Beispiele zur verdeutlichung und mögliche Übungsaufgaben:
a)
![]() b)
b) ![]()
![]() c)
c) ![]()
d) Wenn aus einem 27 Schüler starken Mathekurs eine dreier-Gruppen für eine Refereat ausgewählt wird. Wieviele verschiedene gruppen kann man bilden ?
![]()
e) Wie hoch ist die warscheinlichkeit das die 3 Klassenbesten durch Zufall zusammen kommen ? 1: 29250
f) Wieviel 2 stellige Zahlen lassen sich aus den Ziffern
1, 3, 5, 7, 9 bilden, wenn Ziffernwiederholung verboten ist? ![]()
g) Beim Lotto werden von 49 Zhalen 6 gezogen. Wieviel Kombinatioen zu je 6 gibt es
![]()
-9-
Der binomische Lehrsatz
Mit Hilfe des binomischen Lehrsatzes lassen sich höhere Potenzen von Binomen berechnen.Im Mittelalter formuliert, wurde der binomische Lehrsatz (um 1676) von dem englischen Naturwissenschaftler Sor Isaac Newton auf gebrochene Exponenten verallgemeinert. Dadurch war er in der Lage, seine neu entdeckten Methoden der lnfinitesimalrechnung auf viele komplizierte Probleme anzuwenden. Der binomische Lehrsatz spielt in verschiedenen Bereichen der Mathematik eine Rolle, insbesondere in der Wahrscheinlichkeitstheorie.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
Pascalsches Dreieck, eine dreieckförmige Anordnung von natürlichen Zahlen. In diesem Dreieck entspricht jede Zahl der Summe der beiden ihr am nächsten stehenden Zahlen der vorigen Reihe. Man erhält die Zahlen aber auch durch Berechnung der Koeffizienten der jeweiligen Potenzen des Ausdrucks (x + y),
(x + y)1, (x + y)2 usw., wie es die Abbildung "Pascalsches Dreieck" illustriert.
Die Zeilen werden von oben nach unten durchnumeriert:
n = 0, 1, 2, ... Die Zahlen in der Zeile n entsprechen den Koeffizienten,
die man beim Ausmultiplizieren des jeweiligen Ausdrucks (x + y)n
erhält. Diese Binomialkoeffizienten lassen sich auch folgendermaßen berechnen:

-10-
Veranschaulichung:
1 n=1
1 1 n=2
1 2 1 n=3
1 3 3 1 n=4
1 4 6 4 1 n=5
1 5 10 10 5 1 n=6
1 6 15 20 15 6 1 n=7
(a+b)5 Þ 1 4 6 4 1
![]()
Þ a4 + 4a3b + 6a2b2 + 4ab3 + b4
Die Exponenten von a werden hinuntergezählt, wehrend die Exponenten von b von 0-4 hochgezählt werden ( es hängt von der Anzahl der Zahlen der reihe jeweils ab).
Durch ausrechnen und vergleichen läst sich aus den folgenen Termen folgene Beziehung erkennnen:

Dies legt die Behauptung nahe

-11-
Beweis:
"Beweis für n = 5 (...): Beim Auflösen der Klammern
in dem Produkt (a1+b1)(a2+b2)(a3+b3)(a4+b4)(a5+b5) entstehen Summanden, von
denen jeder 5 Faktoren enthält, und zwar aus jeder der 5 Klammern entweder einen
Faktor a oder einen Faktor b. Es kommen somit in jedem Summanden die 5 Indices
1,2,3,4,5 vor. Man erhält also z.B so viele Summanden mit je 2 Faktoren b wie
es Kombinationen der 5 Faktoren b wie es Kombinationen der 5 Elemente 1,2,3,4,5
zu je zweien gibt,, das sind aber ![]() =
10 Kombinationen, nämlich die 10 Teilprodukte b1b2. b1b3, (...). Ihre Entstehung
zeigt Fig. 35.1. (...)
=
10 Kombinationen, nämlich die 10 Teilprodukte b1b2. b1b3, (...). Ihre Entstehung
zeigt Fig. 35.1. (...)
Beweis für die Hochzahl n: Löst man in (a1+b1)(a2+b2)(a3+b3)...(an+bn)
die Klammern durch Ausmultiplizieren auf, so enthalten die entstehenden Summanden
aus jeder der n Klammern entweder einen Faktor a oder einen Faktor b. Es kommen
daher so viele Summanden mit k Faktoren b vor, wie es Kombinationen von n Elementen
zu je k gibt, also sind es ![]() solche
Summanden. Setzt man nun a1 = a2 = a3 =...
= an und b1 = b2 =b3 =... = bn
, so geht das obige Produkt über in (a+b)n. Jeder Summand mit k Faktoren
b geht über in an-k x bk; dieser Summand tritt daher
solche
Summanden. Setzt man nun a1 = a2 = a3 =...
= an und b1 = b2 =b3 =... = bn
, so geht das obige Produkt über in (a+b)n. Jeder Summand mit k Faktoren
b geht über in an-k x bk; dieser Summand tritt daher ![]() mal auf.
mal auf.
Bemerkungen: (...) 2. Wegen ihres Vorkommens beim
binomischen Satz nennt man die Zahlen ![]() auch
Binomialkoeffizienten. Häufig bezeinet man sie auch als Pascalzahlen."
auch
Binomialkoeffizienten. Häufig bezeinet man sie auch als Pascalzahlen."
Beispiele: ![]()
=a7 + 7a6b + 21a4b3 + 35a3b4+21a2b5 + 7ab6+b7
1,25=![]()
=1+5 x 0,2+10 x 0,04+10 x 0,008+5 x 0,0016+0,00032 = 2,48832
-12-
Mögliche Aufgaben zum Paskalischen Dreieck
8.a) (2 x b)6 = 25 + 5 x 24 x b1+ 10 x 23 x b2 + 10 x 22 x b3 + 5 x 2 x b4 + 5 x b5
b.) (5xb)7
c.) (dxb)3
d.) (5+2 x ba)4
e.) (5a x c)3