von Thorsten Niggemann
Sadi Carnot stellte 1824 fest: „Überall wo ein Temperaturunterschied herrscht, kann mit Hilfe einer Maschine Energie erzeugt werden."
Ein idealer Kreisprozess würde von einer Wärmemaschine mit perfektem Wirkungsgrad ausgeführt werden d. h., die ganze Wärme würde in mechanische Arbeit umgewandelt werden. Aber Sadi Carnot selbst bewies im 19. Jahrhundert, daß es eine ideale Wärmemaschine nicht geben kann. Jede Wärmemaschine muss einen Teil der ihr zugeführten Wärme in Abwärme umwandeln. Der 2. Hauptsatz der Thermodynamik setzt eine obere Grenze für den Wirkungsgrad von Maschinen fest; diese obere Grenze liegt unterhalb von 100 Prozent.
Der Grenzfall wird als Carnot'scher Kreisprozess bezeichnet.
Beim Carnot-Kreisprozeß wird also der größte überhaupt mögliche Anteil der zugeführten Wärme in Nutzarbeit umgewandelt. Somit dient dieser als idealer Vergleichsprozeß zur Beurteilung für den Stirling-Prozeß.
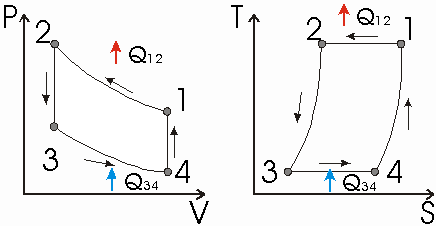
Hier wird der Carnot-Prozeß als links drehender Kreisprozeß (Arbeitsprozeß) dargestellt:

Im Vergleich zum Stirling-Motor wird der Prozeß bei der Stirling-Kältemaschine linksrum durchlaufen. Die Verdichtung mit gleichzeitiger Wärmeabgabe findet auf dem hohen Temperaturniveau statt (l à 2). Die höhere der beiden Temperaturen des Stirling-Kreisprozesses ist also die Temperatur der Kompression tc , die typischerweise in der Nähe der Umgebungstemperatur, also zum Beispiel bei 45°C liegt. Im Anschluß an die Verdichtung wird das komprimierte Arbeitsgas isochor in den Expansionsraum übergeschoben, wobei es im Regenerator Wärme abgibt und sich dadurch abkühlt (2 à 3). Im Expansionsraum wird das Arbeitsgas unter gleichzeitiger Wärmeaufnahme bei der tiefen Expansionsraumtemperatur TE , die deutlich unterhalb der Umgebungstemperatur. beispielsweise bei -50°C liegt, entspannt
(3 à 4). Dabei wird in der Umgebung, aus der die Wärme vom Arbeitsgas aufgenommen wird, Kälte erzeugt. Der Kreisprozeß wird dann durch das Überschieben des expandierten Gases in den Kompressionsraum, bei dem das Gas im Regenerator Wärme aufnimmt, geschlossen (4 à 1).
p - V und T -s Diagramm des idealen Stirling Kältemaschinen Prozesses
Bei jeder Zyklushälfte durchströmt das Arbeitsgas den Regenerator, dabei nimmt es in der ersten Zyklushälfte die Wärme des Regenerator auf und gibt sie in der zweiten Zyklushälfte wieder an den Regenerator ab. Der Regenerator dient somit als thermische Speichermasse.
Für den idealen Regenerator gilt:
Auf seiner linken Seite hat er die niedrige Temperatur des Kompressionsraumes und auf seiner rechten Seite die hohe Temperatur des Expansionsraumes. Innerhalb des Regenerator verläuft die Temperatur linear.
Die Wärmekapazität des Regenerator ist so hoch, daß sich die Regeneratortemperatur nicht ändert.
Während das Arbeitsgas den Regenerator durchströmt, haben Regenerator und Arbeitsgas überall die gleiche Temperatur.
Der Regenerator bietet dem Arbeitsgas keinen Strömungswiderstand.
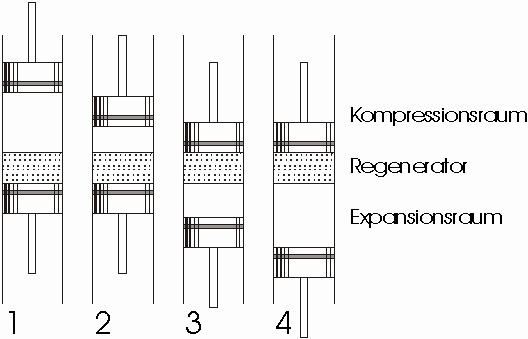
Zustandsänderungen:
3 à 4 Isotherme Kompression; Wärmeabfuhr nach außen; Arbeitszufuhr von außen.
4 à 1 Isochore innere Wärmezufuhr vom Regenerator ( Verdrängerkolben ).
1 à 2 Isotherme Expansion; Wärmezufuhr von außen; Arbeitsabfuhr nach außen.
2 à 3 Isochore innere Wärmeabfuhr an der Regenerator ( Verdrängerkolben ).
Für die vom Arbeitsgas aufgenommene Wärme aus dem tiefen Temperaturbereich gilt:
(...)
Das Verhältnis zwischen Nutzen und Aufwand bei der Kältemaschine bezeichnet man als Kälteleistungszahl e . Diese beinhaltet die vom Arbeitsgas aufgenommene Wärme und die von außen zugeführte Arbeit.
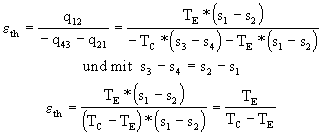
Das Verhältnis der Leistungszahl einer ausgeführten Sterling-Maschine zur Carnot-Leistungszahl ist ein Merkmal für die Güte der Konstruktion der Maschine. Je höher das Verhältnis ausfällt, desto effektiver nutzt die Maschine die eingesetzte Energie.
Der im vorherigen Kapitel beschriebene Ideale Stirling-Prozeß ist natürlich nicht erreichbar.
Die nachfolgenden aufgelisteten Punkte gehen auf die wichtigsten Abweichungsmerkmale ein.
Um den Kälteprozeß so gut wie möglich auszufahren, müssen die Toträume so klein wie möglich gehalten werden.
(...)
Dazu währe eine diskontinuierliche Kolbensteuerung nötig.
Das heißt: Während der Kompression verharrt der Expansionskolben in Ruhe und während der Expansion bewegt sich der Kompressionskolben nicht. Wenn sich die Kolben bewegen, so erfolgt ihre Bewegung mit konstanter Geschwindigkeit.
Dieser Vorgang ist in einigen Sonder fällen nur begrenzt erreichbar und mit den Nachteilen von Geräuschentwicklung und hohen mechanischen Belastungen verbunden.
Vergleich von kontinuierlicher und diskontinuierlicher Kolbenbewegung bei zwei gegeneinander phasenverschobenen sinusförmigen Kolbenbewegungen .
Deshalb wird eine sinusförmige Kolbenbewegung, die auch bei hoher Drehzahl einen ruhigen Lauf ermöglicht angewandt. Die übliche Phasenverschiebung zwischen Expansionskolben und Kompressionskolben beträgt 90°, sie kann aber auch 120° betragen. Was besser geeignet ist kann nur durch Optimierung heraus gefunden werden.
Die Isotherme Zustandsänderung wird nicht erreicht, da bei einer Antriebsdrehzahl von 1000 U/min der Kreisprozeß ca.17 mal in der Sekunde durchlaufen wird. So findet keine isotherme sondern eine adiabate Zustandsänderung statt. Eine Annäherung an die Isotherme kann nur durch verbesserte Wärmeübertragung und niedriger Drehzahl erreicht werden.
Während das Arbeitsgas vom heißen in den kalten Raum über den Regenerator strömt, heizt dieser das Arbeitsgas auf und kühlt es in der zweiten Zyklushälfte wieder ab. Bei diesem Vorgang ändert der Regenerator natürlich seine eigene Temperatur. Außerdem ist der Wärmeübergang vom Regenerator auf das Arbeitsgas nicht ideal, so daß immer ein geringer Temperaturunterschied von Regenerator und Arbeitsgas vorhanden ist. Das hat zur Folge, daß der Kühler eine große Wärmemenge abführen muß und der Freezer ( bei der Arbeitsmaschine = Erhitzer ) eine geringere Wärmemenge aufnehmen kann.
Im Idealfall befindet sich das gesamte Arbeitsmedium im Expansions- und Kompressionsraum. Jedoch besitzen reale Maschinen einen Totraum, in ihrem Wärmetauscheraggregat, bestehend aus: Freezer (Erhitzer), Regenerator und Kühler. In diesen Toträumen ändert sich das Volumen während des Kreisprozeßzyklusses in der Maschine nicht. Die Folge ist eine verringerte Kälteleistung in der Kältemaschine
(...)
Der GesamtverlustVerluste durch Dissipation, bedeuten das durch die Umwandlung von nutzbarer Energie wie: kinetische-, mechanische- oder Druckenergie in innere Energie, sich die Leistungszahl des Kälte Prozess verschlechtert.
Dissipation findet auch durch Druckverluste im Arbeitsgas statt, da es nicht möglich ist die bewegten Teile völlig abzudichten entweicht da unter hohen Druck befindlichen Arbeitsgas (vor allem Wasserstoff oder Helium) in die Umgebung. Hier kann langfristig ein großer Leistungsanteil verloren gehen.
Bei der Dissipation durch ein reales Gas sind Stömungsverluste, hauptsächlich durch Verwirbelung im Regenerator, gemeint. Aber auch die innere Reibung der Gase, die dadurch Exergie in Anergie wandeln, die dann als nicht nutzbare Wärme abgeführt werden muss. Es findet eine irreversible Zustandsänderung statt.
Bei der Dissipation durch mechanische Reibung, treten Verluste an allen mechanische Reibflächen wie Lager, Zylinderwand, usw. auf, wobei mechanische Exergie in Reibungswärme (Anergie) umgewandelt wird.
Wärmeleitungsverluste entstehen durch einen Wärmestrom in Richtung des Temperaturgefälles längst des Zylinders und nach außen. Diese Verluste Lassen sich durch eine geeignete Materialwahl verringern.
Wärmeleitungsverluste entstehen auch durch die Bewegung des Kolbens oder Verdrängers. Befindet sich der Verdränger in einer der beiden Totlagen, so entsteht jeweils ein Wärmestrom über die Zylinderwand in Richtung des Temperaturgefälles. Diesen Effekt könnte auch durch einen kürzeren Hub verringert werden, aber dann würden Zylinderdurchmesser und damit auch die Wärmeverluste längst des Zylinders wieder ansteigen. Dieser Pendelverlust wird auch als Shuttle-Verlust bezeichnet.
Um eine ideale Wärmeaufnahme bzw. -abgabe zu erreichen müßte die Zylinderfläche unendlich groß sein. Bei einem Zylinder ist die Volumenbezogene Oberfläche aber ziemlich klein. Somit kann nur eine bestimmte Wärmemenge über die Zylinderwand übertragen werden. Große Temperaturdifferenzen bei der Wärmeübertragung aber führen gemäß dem zweiten Hauptsatz der Thermodynamik zu Exergieverlusten und damit zu einer Verschlechterung der Leistungszahl der Stirling-Maschine. Um eine bessere Lestungszahl zu erreichen werden zusätzliche Wärmeübertrager eingesetzt, die aber auch ein zusätzliches Totvolumen besitzen.
Die Auswirkung aller vorher aufgeführten Verluste ist im folgenden p -V Diagramm dargestellt. Der zu erwartende Wirkungsgrad einer Stirling - Maschine neuerer Bauart liegt bei etwa 40% .

Klassifizierung der Stirling-Maschine
Um einen Überblick über die Vielzahl der verschiedenen Stirling-Maschine zu erhalten ist es
sinnvoll diese zu Klassifizieren. Wie diese Klassifizierung durchgeführt wird ist nicht festgelegt, es ist nicht einfach Einteilungsmerkmale zu finden und aufzustellen, da sich hier und da Widersprüche bei der Einteilung ergeben. Um dennoch eine Einteilung vornehmen zu können werden die Stirling-Maschinen in vier grundschemata aufgeteilt:
- Maschinenbauart
- Zylinderraumzuordnung
- Art des Zusammenwirkens der Kolben
- Kolbenart, Antriebs- und Getriebespezifikation
Diese Einteilung erhebt keine Anspruch auf Vollständigkeit, Verfeinerungen sind durchaus noch möglich.
Thermodynamische Berechnungsgrundlagen von Stirling-Maschinen
Die Berechnungsverfahren von Stirling-Maschinen werden in der Literatur in 4 Klassen eingeteilt, man spricht auch von 0. bis 3.Ordnung.
0.Ordnung
Bei der Auslegung der Stirling-Maschine wird mit Hilfe von Diagrammen sogenannte „Desigen Charts" ermöglicht. Zum Beispiel das Verhalten der Leistung oder des Wirkungsgrades einer Stirling-Maschine in Abhängigkeit von verschiedenen frei wählbaren konstruktiven Größen. Dieses Verfahren beruht auf dem gesammelten Know-How in konzentrierter Form, es ist zur Auslegung aber nicht zur Optimierung geeignet.
1.Ordnung
Der Schmidt Zyklus ist als Analyse Verfahren der 1.Ordnung bekannt, er bezieht sich auf einem Stirling Prozeß mit sinusförmiger Kolbenbewegung.
2.Ordnung
Die Analyse der 2.Ordnung erfordert den Computereinsatz, da der Berechnung ein idealer adiabater Zyklus zugrundeliegt. Der Wärmeübergangskoeffizient kann hier von adiabat (gleich Null) bis isotherm (gleich unendlich) variiert werden.
3.Ordnung
Im Computerprogramm der 3.Ordnung werden gekoppelte Bilanzgleichungen für Masse, Impuls und Energie des Arbeitsgases mittels verschiedener numerischer Verfahren gelöst. Die von mir durchgeführte thermodynamische Auslegung basiert auf dem Carnotprozess. Tiefer gehende Berechnungen erfordern einiges mehr an Rechenaufwand und Zeit und konnten von mir nicht weiter verfolgt werden.
Volumenberechnung
Maximales Volumen des Verdrängerkolbens
![]()
Maximales Volumen des Kompressionskolbens
(...)
VE [m3] = Volumen des Verdrängers
VC [m3] = Volumen des Kompressors
rE [m] = Radius des Verdrängerkolbens
rC [m] = Radius des Kompressionskolbens
r[m] = Länge der Kurbelschwinge Hub = 2 * r
Totraum des Regenerators
![]()
rreg [m] = Radius des Regenerators
Volumenänderung in Abhängigkeit a des Kurbelwinkels
(...)
Gesamtvolumen in Abhängigkeit a des Kurbelwinkels
![]()
Berechnung aller Zustandsgrößen von Punkt 1 - 4
Punkt 2.
Der Punkt 2 ist die Startposition, hier wird der Fülldruck vorgegeben, daraus kann die Masse des sich in der Maschine befindlichen Arbeitsmedium bestimmt werden.
(...)
mgas [Kg] = Masse des Gases
T2 [K] = Umgebungstemperatur
p2 [pa] = Fülldruck
V2 [m3] = Volumen bei 90°
RL = spezielle Gaskonstante
Punkt 3.
Isochore Wärmeabfuhr
Punkt 4.
Isotherme Entspannung
Punkt 1.
Isochore Wärmezufuhr
![]()
Zugeführte Wärme von 3. nach 4.
Q34 [kW] = Zugeführte Wärme
Abgeführte Wärme von 1. nach 2.
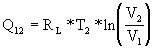
Q12 [kW] = Abgeführte Wärme
Die während des Prozesses geleistete Arbeit
Wt [kW] = geleistete Arbeit
Um so näher der Wirkungsgrad h an 1 kommt, um so besser ist der geleistete Prozeß
![]()
Berechnung der benötigten elektrischen Antriebsleistung